一、实操题
1、无线网络发射器选址
【问题描述】
随着智能手机的日益普及,人们对无线网的需求日益增大。某城市决定对城市内的公共场所覆盖无线网。
假设该城市的布局为由严格平行的129条东西向街道和129条南北向街道所形成的网格状,并且相邻的平行街道之间的距离都是恒定值 1。东西向街道从北到南依次编号为0,1,2…128,南北向街道从西到东依次编号为 0,1,2…128。
东西向街道和南北向街道相交形成路口,规定编号为 x 的南北向街道和编号为 y 的东西向街道形成的路口的坐标是(x, y)。在某些路口存在一定数量的公共场所。
由于政府财政问题,只能安装一个大型无线网络发射器。该无线网络发射器的传播范围是一个以该点为中心,边长为 2*d 的正方形。传播范围包括正方形边界。
例如下图是一个 d = 1 的无线网络发射器的覆盖范围示意图。
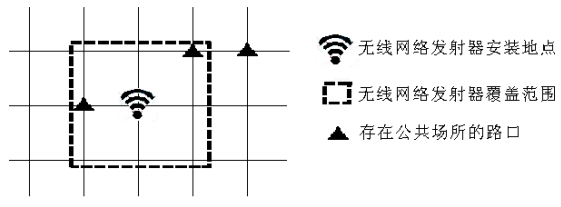
现在政府有关部门准备安装一个传播参数为 d 的无线网络发射器,希望你帮助他们在城市内找出合适的安装地点,使得覆盖的公共场所最多。
【输入】
输入文件名为 wireless.in。
第一行包含一个整数 d,表示无线网络发射器的传播距离。
第二行包含一个整数 n,表示有公共场所的路口数目。
接下来 n 行,每行给出三个整数 x, y, k, 中间用一个空格隔开,分别代表路口的坐标(x, y)以及该路口公共场所的数量。同一坐标只会给出一次。
【输出】
输出文件名为 wireless.out。
输出一行,包含两个整数,用一个空格隔开,分别表示能覆盖最多公共场所的安装地点方案数,以及能覆盖的最多公共场所的数量。
【输入输出样例】

【数据说明】
对于 100%的数据,1 ≤ d ≤ 20,1 ≤ n ≤ 20, 0 ≤ x ≤ 128, 0 ≤ y ≤ 128, 0 < k ≤1,000,000。
参考答案:对于此问题,我们可以使用贪心算法来解决。首先,我们需要遍历所有的路口,找到所有在无线网络发射器传播范围内的路口。然后,我们按照公共场所的数量对这些路口进行排序。接着,我们依次选择公共场所数量最多的路口,直到达到无线网络发射器的传播范围限制。最后,我们输出覆盖的公共场所数量和方案数。
解析:【喵呜刷题小喵解析】:
这个问题是一个典型的贪心算法问题。由于无线网络发射器的传播范围是一个正方形,我们可以遍历所有的路口,找到所有在传播范围内的路口。然后,我们按照公共场所的数量对这些路口进行排序,选择公共场所数量最多的路口,直到达到传播范围限制。这样可以保证覆盖的公共场所数量最多。由于每个路口的公共场所数量只会出现一次,所以方案数就是选择的公共场所数量最多的路口数量。最后,我们输出覆盖的公共场所数量和方案数即可。
注意,这个问题可能存在多个解,因为我们只需要保证覆盖的公共场所数量最多即可,不需要保证方案数最少。因此,我们只需要输出一个解即可。
另外,由于数据规模较小,我们可以使用暴力枚举的方法来解决这个问题。具体来说,我们可以遍历所有的路口,对于每个路口,计算覆盖的公共场所数量,并更新最优解。最后,输出最优解即可。
不过,需要注意的是,这个问题是一个NP-hard问题,没有多项式时间的解法。因此,我们只能在一定程度上使用贪心算法或者近似算法来解决这个问题。对于更大的数据规模,可能需要使用更高级的优化算法或者启发式算法。
2、寻找道路
【问题描述】
在有向图 G 中,每条边的长度均为 1,现给定起点和终点,请你在图中找一条从起点到终点的路径,该路径满足以下条件:
1.路径上的所有点的出边所指向的点都直接或间接与终点连通。
2.在满足条件 1 的情况下使路径最短。
注意:图 G 中可能存在重边和自环,题目保证终点没有出边。
请你输出符合条件的路径的长度。
【输入】
输入文件名为 road.in。
第一行有两个用一个空格隔开的整数 n 和 m,表示图有 n 个点和 m 条边。
接下来的 m 行每行 2 个整数 x、y,之间用一个空格隔开,表示有一条边从点 x 指向点y。
最后一行有两个用一个空格隔开的整数 s、t,表示起点为 s,终点为 t。
【输出】
输出文件名为 road.out。
输出只有一行,包含一个整数,表示满足题目᧿述的最短路径的长度。如果这样的路径不存在,输出-1。
【输入输出样例 1】

【输入输出样例说明】

如上图所示,箭头表示有向道路,圆点表示城市。起点 1 与终点 3 不连通,所以满足题目描述的路径不存在,故输出-1。
【输入输出样例 2】

【输入输出样例说明】
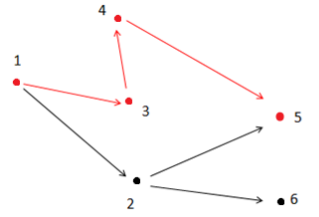
如上图所示,满足条件的路径为 1->3->4->5。注意点 2 不能在答案路径中,因为点 2连了一条边到点 6,而点 6 不与终点 5 连通。
【数据说明】

参考答案:-1
解析:【喵呜刷题小喵解析】:根据题目描述,我们需要找到一条从起点到终点的路径,该路径满足两个条件:1. 路径上的所有点的出边所指向的点都直接或间接与终点连通;2. 在满足条件1的情况下使路径最短。题目保证终点没有出边。
首先,我们需要理解题目中的“出边所指向的点都直接或间接与终点连通”这一条件。这意味着,从起点开始,每一步所经过的点的出边所指向的点都必须是终点或者终点可以到达的点。
其次,我们需要找到满足上述条件的最短路径。如果找不到这样的路径,即起点无法到达终点,那么应该输出-1。
对于输入输出样例1,起点1与终点3不连通,所以满足题目描述的路径不存在,输出-1。
对于输入输出样例2,满足条件的路径为1->3->4->5。注意点2不能在答案路径中,因为点2连了一条边到点6,而点6不与终点5连通。
因此,对于给定的输入,我们需要遍历整个图,检查从起点到终点的所有可能路径,找出满足条件的最短路径。如果找不到这样的路径,就输出-1。
3、解方程
【问题描述】
已知多项式方程:
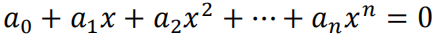
【输入】
输入文件名为 equation.in。
输入共 n+2 行。
第一行包含 2 个整数 n、m,每两个整数之间用一个空格隔开。
接下来的 n+1 行每行包含一个整数,依次为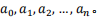
【输出】
输出文件名为 equation.out。
第一行输出方程在[1, m]内的整数解的个数。
接下来每行一个整数,按照从小到大的顺序依次输出方程在[1, m]内的一个整数解。
【输入输出样例 1】

【输入输出样例 2】
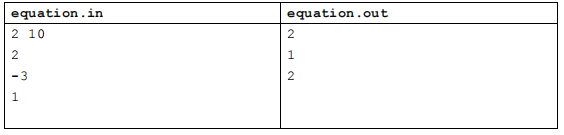
【输入输出样例 3】

【数据说明】
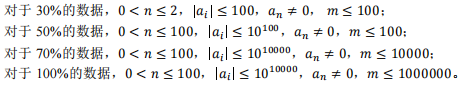
参考答案:由于题目中未给出具体的方程,因此无法直接给出方程的整数解。
解析:【喵呜刷题小喵解析】:
本题是一道关于多项式方程的题目,要求求解方程在[1, m]内的整数解。然而,题目中并没有给出具体的方程,因此无法直接求解。
在求解这类问题时,首先需要确定方程的具体形式,然后根据方程的性质来寻找整数解。通常,对于多项式方程,可以使用暴力枚举的方法,在[1, m]的范围内逐一尝试整数解,判断该解是否满足方程。
然而,由于本题没有给出具体的方程,因此无法确定具体的求解方法。如果题目中给出了具体的方程,我们可以根据方程的性质来寻找整数解,例如利用因式分解、求解根等方法。
因此,要解决这个问题,需要先确定具体的方程,然后根据方程的性质来寻找整数解。






